Regular tree grammar
In Computer Science, a regular tree grammar (RTG)[1] is a formal grammar that describes a set of directed trees.
Contents |
Definition
A regular tree grammar  is defined by the tuple
is defined by the tuple
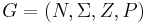 ,
,
where
 is a set of nonterminals,
is a set of nonterminals, is a ranked alphabet (i.e., an alphabet whose symbols have an associated arity) disjoint from
is a ranked alphabet (i.e., an alphabet whose symbols have an associated arity) disjoint from  ,
,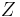 is the starting nonterminal, with
is the starting nonterminal, with 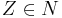 , and
, and is a set of productions of the form
is a set of productions of the form 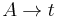 , where
, where 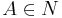 , and
, and 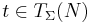 , where
, where 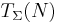 is the associated term algebra.
is the associated term algebra.
Derivation of Trees
The grammar  implicitly defines a set of trees: any tree that can be derived from
implicitly defines a set of trees: any tree that can be derived from 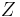 using the rule set
using the rule set  is said to be described by
is said to be described by  . This set of trees is known as the language of
. This set of trees is known as the language of  . To express this more formally, we define the relation
. To express this more formally, we define the relation 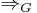 on the set
on the set 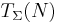 as follows:
as follows:
For every 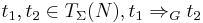 , if there is a context
, if there is a context 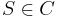 and a production
and a production 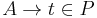 such that:
such that:
![t_1 = S[A]](/2012-wikipedia_en_all_nopic_01_2012/I/d9f0c58110a10a43b2917023ccc98ccd.png) , and
, and![t_2 = S[t]](/2012-wikipedia_en_all_nopic_01_2012/I/bbe95d2590e39d41828ec733e7c03890.png) .
.
The tree language generated by  is the language
is the language
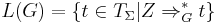 .
.
Where 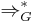 denotes successive applications of
denotes successive applications of 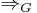 . Such languages are called Tree languages.
. Such languages are called Tree languages.
Relation to other formal languages
As shown by Rajeev Alur and Parthasarathy Madhusudan[2][3] the class of regular tree languages coincides with nested words and visibly pushdown languages.
See also
References
- ^ psu.edu - Regular tree grammars as a formalism for scope underspecification
- ^ Alur, R.; Madhusudan, P. (2004). Visibly pushdown languages. pp. 202. doi:10.1145/1007352.1007390.
- ^ Alur, R.; Madhusudan, P. (2009). "Adding nesting structure to words". Journal of the ACM 56 (3): 1–43. doi:10.1145/1516512.1516518.